Most of the students fresh out of their engineering studies or those who are still studying will have the concept of Binary Search Trees fresh in their minds. But with most of the people who have been out of college for many years now will kind of be having a not so clear idea of Binary Search trees unless they have been using it or related concepts at their work. Also you can read the extensive concepts about this topic on any of the popular data structure book in the store.
books:
In this tutorial I would show how to implement a Binary Search Tree (BST) in Java and also show the following operations:
- Inserting/Building a BST
- Finding maximum value node in BST
- Finding minimum value node in BST
- Inorder Traversal of BST
- Preorder Traversal of BST
- Postorder Traversal of BST
What is a Binary Search Tree (BST)?
Binary Search Tree (BST) is a binary tree data structure with a special feature where in the value store at each node is greater than or equal to the value stored at its left sub child and lesser than the value stored at its right sub child. Lets look at an example of a BST:
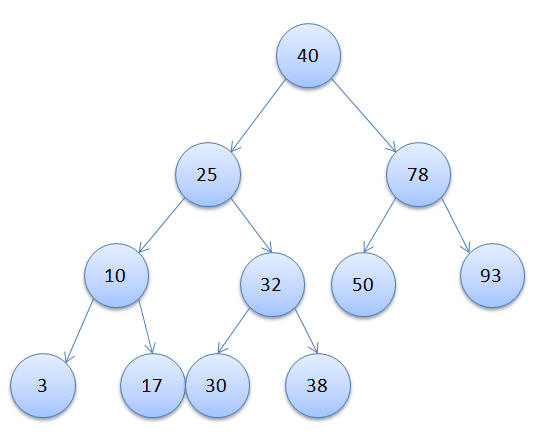
In the above example you can see that at each node the value in the left child is lesser than or equal to the value in the node and the value in the right child is greater than the value in the node.
Building a Binary Search Tree (BST)
Now that we have seen how a BST looks, let me show you how one can build a BST and insert nodes into the tree by implementing the algorithm in Java. The basic idea is that at each node we compare with the value being inserted. If the value is lesser then we traverse through the left sub tree and if the value is greater we traverse through the right subtree. Suppose we have to insert the value 64 in the above BST, lets look at the nodes traversed before its inserted at the right place:
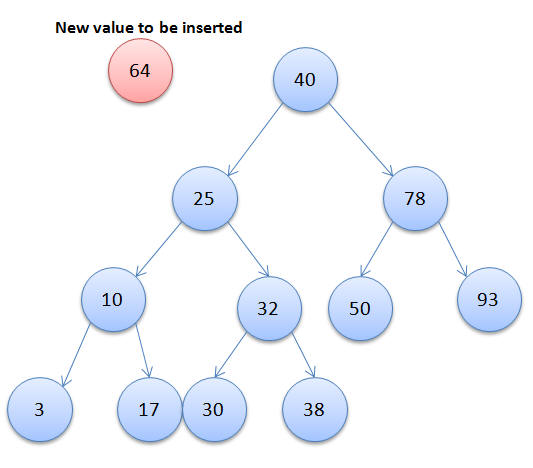
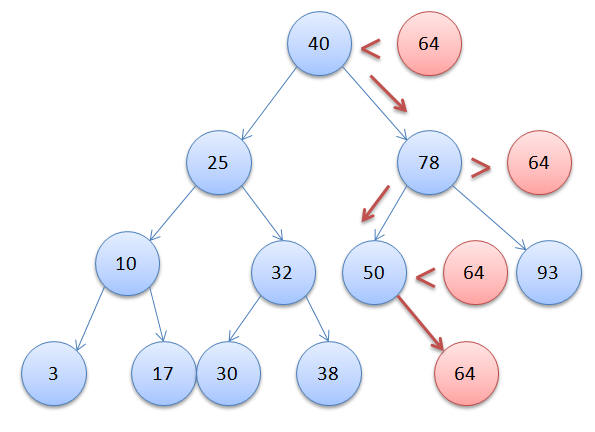
Each node in the BST is represented by the below java class:
public class Node<T> {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
}
Lets look at the code in Java for achieving the above logic:
public class BinarySearchTree {
public Node root;
public void insert(int value){
Node node = new Node<>(value);
if ( root == null ) {
root = node;
return;
}
insertRec(root, node);
}
private void insertRec(Node latestRoot, Node node){
if ( latestRoot.value > node.value){
if ( latestRoot.left == null ){
latestRoot.left = node;
return;
}
else{
insertRec(latestRoot.left, node);
}
}
else{
if (latestRoot.right == null){
latestRoot.right = node;
return;
}
else{
insertRec(latestRoot.right, node);
}
}
}
}
Finding Maximum and Minimum Value in BST
If you have noticed in the above example that the leftmost node has the lowest value and the rightmost node has the highest value. This is due to the sorted nature of the tree.
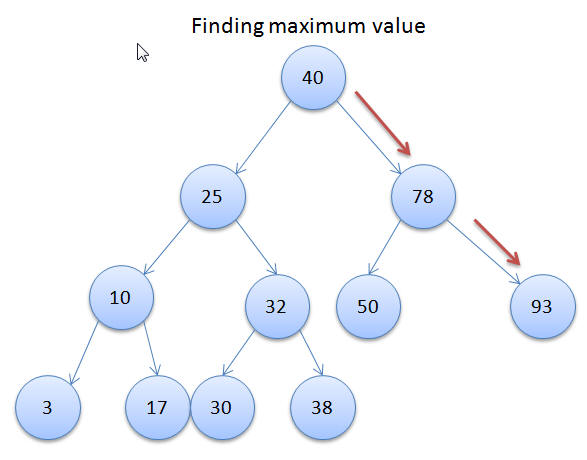
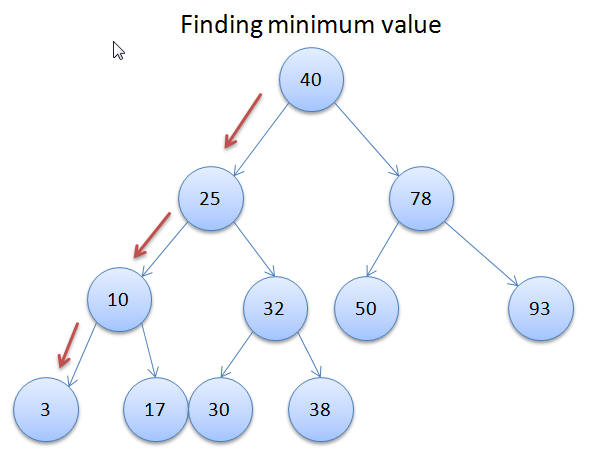
Using this principle the below methods return us the lowest and highest value in the Binary Search Tree:
/**
* Returns the minimum value in the Binary Search Tree.
*/
public int findMinimum(){
if ( root == null ){
return 0;
}
Node currNode = root;
while(currNode.left != null){
currNode = currNode.left;
}
return currNode.value;
}
/**
* Returns the maximum value in the Binary Search Tree
*/
public int findMaximum(){
if ( root == null){
return 0;
}
Node currNode = root;
while(currNode.right != null){
currNode = currNode.right;
}
return currNode.value;
}
Traversing the Binary Search Tree (BST)
Traversing the tree or BST in this case is visiting each of the nodes present in the tree and performing some operation with the value present in the node which in this case will be printing the value present in the node. When we traverse the tree we have to visit the value present in the node, then node’s right sub tree and the left sub tree. Visiting the right and left sub tree will be a recursive operation. The order in which we perform the three operations i.e visiting the value, right sub tree and left sub tree gives rise to three traversal techniques:
- Inorder Traversal
- Preorder Traversal
- Postorder Traversal
Inorder Traversal
In this traversal the left sub tree of the given node is visited first, then the value at the given node is printed and then the right sub tree of the given node is visited. This process is applied recursively all the node in the tree until either the left sub tree is empty or the right sub tree is empty.
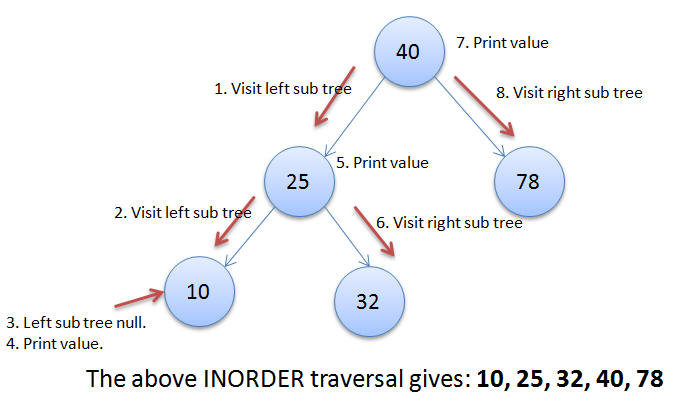
Applying the Inorder traversal for the give example we get: 3, 10, 17, 25, 30, 32, 38, 40, 50, 78, 78, 93.
/**
* Printing the contents of the tree in an inorder way.
*/
public void printInorder(){
printInOrderRec(root);
System.out.println("");
}
/**
* Helper method to recursively print the contents in an inorder way
*/
private void printInOrderRec(Node currRoot){
if ( currRoot == null ){
return;
}
printInOrderRec(currRoot.left);
System.out.print(currRoot.value+", ");
printInOrderRec(currRoot.right);
}
Preorder traversal
In this traversal the value at the given node is printed first and then the left sub tree of the given node is visited and then the right sub tree of the given node is visited. This process is applied recursively all the node in the tree until either the left sub tree is empty or the right sub tree is empty.
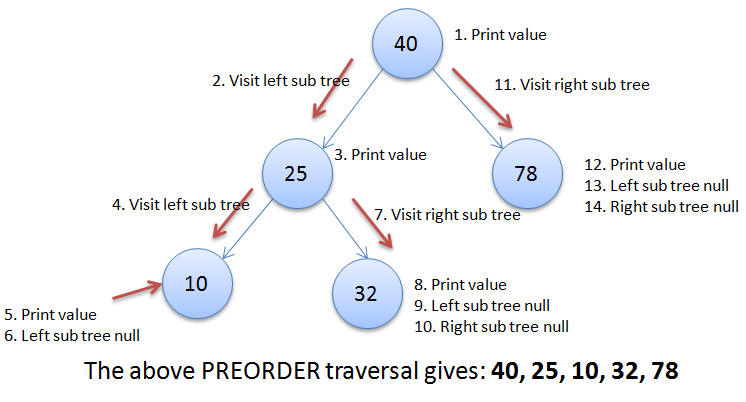
Applying the Preorder traversal for the give example we get: 40, 25, 10, 3, 17, 32, 30, 38, 78, 50, 78, 93.
/**
* Printing the contents of the tree in a Preorder way.
*/
public void printPreorder() {
printPreOrderRec(root);
System.out.println("");
}
/**
* Helper method to recursively print the contents in a Preorder way
*/
private void printPreOrderRec(Node currRoot) {
if (currRoot == null) {
return;
}
System.out.print(currRoot.value + ", ");
printPreOrderRec(currRoot.left);
printPreOrderRec(currRoot.right);
}
Postorder Traversal
In this traversal the left sub tree of the given node is traversed first, then the right sub tree of the given node is traversed and then the value at the given node is printed. This process is applied recursively all the node in the tree until either the left sub tree is empty or the right sub tree is empty.
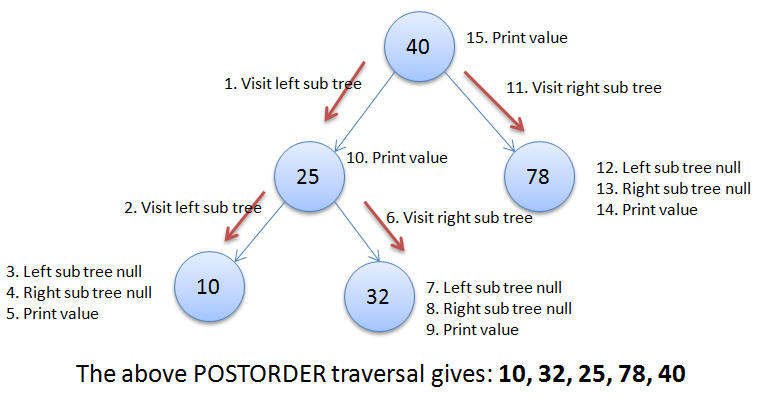
Applying the Postorder traversal for the give example we get: 3, 17, 10, 30, 38, 32, 25, 50, 93, 78, 78, 40.
/**
* Printing the contents of the tree in a Postorder way.
*/
public void printPostorder() {
printPostOrderRec(root);
System.out.println("");
}
/**
* Helper method to recursively print the contents in a Postorder way
*/
private void printPostOrderRec(Node currRoot) {
if (currRoot == null) {
return;
}
printPostOrderRec(currRoot.left);
printPostOrderRec(currRoot.right);
System.out.print(currRoot.value + ", ");
}
The complete code which builds the tree for the example explained in this code and prints the maximum, minimum value, inorder traversal, preorder traversal and post order traversal can be found below:
/**
* Represents a node in the Binary Search Tree.
*/
public class Node<T> {
//The value present in the node.
public int value;
//The reference to the left subtree.
public Node left;
//The reference to the right subtree.
public Node right;
public Node(int value) {
this.value = value;
}
}
/**
* Represents the Binary Search Tree.
*/
public class BinarySearchTree {
//Refrence for the root of the tree.
public Node root;
public BinarySearchTree insert(int value) {
Node node = new Node<>(value);
if (root == null) {
root = node;
return this;
}
insertRec(root, node);
return this;
}
private void insertRec(Node latestRoot, Node node) {
if (latestRoot.value > node.value) {
if (latestRoot.left == null) {
latestRoot.left = node;
return;
} else {
insertRec(latestRoot.left, node);
}
} else {
if (latestRoot.right == null) {
latestRoot.right = node;
return;
} else {
insertRec(latestRoot.right, node);
}
}
}
/**
* Returns the minimum value in the Binary Search Tree.
*/
public int findMinimum() {
if (root == null) {
return 0;
}
Node currNode = root;
while (currNode.left != null) {
currNode = currNode.left;
}
return currNode.value;
}
/**
* Returns the maximum value in the Binary Search Tree
*/
public int findMaximum() {
if (root == null) {
return 0;
}
Node currNode = root;
while (currNode.right != null) {
currNode = currNode.right;
}
return currNode.value;
}
/**
* Printing the contents of the tree in an inorder way.
*/
public void printInorder() {
printInOrderRec(root);
System.out.println("");
}
/**
* Helper method to recursively print the contents in an inorder way
*/
private void printInOrderRec(Node currRoot) {
if (currRoot == null) {
return;
}
printInOrderRec(currRoot.left);
System.out.print(currRoot.value + ", ");
printInOrderRec(currRoot.right);
}
/**
* Printing the contents of the tree in a Preorder way.
*/
public void printPreorder() {
printPreOrderRec(root);
System.out.println("");
}
/**
* Helper method to recursively print the contents in a Preorder way
*/
private void printPreOrderRec(Node currRoot) {
if (currRoot == null) {
return;
}
System.out.print(currRoot.value + ", ");
printPreOrderRec(currRoot.left);
printPreOrderRec(currRoot.right);
}
/**
* Printing the contents of the tree in a Postorder way.
*/
public void printPostorder() {
printPostOrderRec(root);
System.out.println("");
}
/**
* Helper method to recursively print the contents in a Postorder way
*/
private void printPostOrderRec(Node currRoot) {
if (currRoot == null) {
return;
}
printPostOrderRec(currRoot.left);
printPostOrderRec(currRoot.right);
System.out.print(currRoot.value + ", ");
}
}
public class BinarySearchTreeDemo {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst .insert(40)
.insert(25)
.insert(78)
.insert(10)
.insert(3)
.insert(17)
.insert(32)
.insert(30)
.insert(38)
.insert(78)
.insert(50)
.insert(93);
System.out.println("Inorder traversal");
bst.printInorder();
System.out.println("Preorder Traversal");
bst.printPreorder();
System.out.println("Postorder Traversal");
bst.printPostorder();
System.out.println("The minimum value in the BST: " + bst.findMinimum());
System.out.println("The maximum value in the BST: " + bst.findMaximum());
}
}
Summary
In this tutorial you would have got the very clear understanding on how to implement the Binary Search Tree (BST) in Java with various techniques. We have done good enough research on the binary search trees concept before writing this tutorial. I hope you have enjoyed reading this tutorial. If you have any questions, please write it in the comments section.
Have you worked on binary search tree implementation in your company project?. Please share your experience with us.
books:

 Create Buttons using jQuery UI
Create Buttons using jQuery UI